
- 선형 구조: 데이터의 항목 사이의 관계가 1:1 ex)배열, 연결리스트, 스택, 큐
- 비선형 구조: 데이터의 항목 사이의 관계각 1:n 또는 n:m ex) 그래프, 트리
배열
- 엑세스 속도가 빠르다.
- 배열은 삽입 삭제가 어렵고 메모리에 종속적인 것이 단점이다.
- 선형 리스트라고도 한다.
연결리스트
- 연결리스트 임의의 위치에서의 데이터의 삽입과 삭제가 가능하다.
- 노드의 삽입 삭제가 쉽다. 엑세스 속도는 느리다
- 연결리스트를 구현할 경우 자기참고 구 조체에 의해 데이터와 포인터를 저장하는 노드를 구성해야 한다.
- 연결리스트는 배열과 달리 동적 메모리 할당되므로 공간이 부족하여 저장되지 않는 경우는 거의 없다.
- 배열의 다음 데이터를 인덱스를 증가시켜 접근하지만, 연결리스트는 포인터로 접근하므로 다음 데이터가 반드시 연속된 기억공간에 저장될 필요가 없다.
- 삽입이나 삭제 시 선행 노드를 찾기 위해 또 다른 검색이 수행되므로 O(n)시간을 소요하지만, 선행 노드를 알 경우에는 O(1)의 시간복잡도를 갖는다.
스택
- LIFO
큐
- FIFO
- 큐의 크기는 배열을 사용할 경우 미리 정해져있고, 연결리스트를 사용할 경우에는 정해져 있지 않다.
삽입과 삭제의 시간복잡도는 O(1).
정렬
| 정렬 종류 | 평균 수행시간 | 최악 수행시간 | 기억공간 | 비고 |
| 선택 정렬 | O(N^2) | O(N^2) | n | |
| 버블 정렬 | O(N^2) | O(N^2) | n | |
| 삽입 정렬 | O(N^2) | O(N^2) | n | |
| 쉘 정렬 | O(N^2) | O(N^2) | n | 버블 정렬의 단점 보완, 매개변수 이용 |
| 퀵 정렬 | O(nlogn) | O(N^2) | n + stack | 자기 호출 방식 이용 , 성능이 가장 좋음 |
| 2인 합병 정렬 | O(nlogn) | O(nlogn) | 가장 많은 기억 공간 차지 |
|
| 힙 정렬 | O(nlogn) | O(nlogn) | 트리로 표현 | |
| 기수 정렬 | O(k(n + q)) | O(k(n + q)) | (n+1)q = (n+1)r |
- 이미 정렬된 입력 데이터로 O(n)의 시간복잡도를 얻을 수 있는 정렬 기법은 버블과 삽입 정렬이다.
- 퀵 정렬과 합병 졍렬은 분할정복 방법을 사용하는 알고리즘이다.
선택정렬
예) 초기 배열 [9,6,7,3,5]
1회전 결과 [ 3 6 7 9 5 ] <= 최솟값 탐색 3 , 9와 3 교환.
2회전 결과 [ 3 5 7 9 6 ] <= 최솟값 탐색 5, 5와 6교환
3회전 결과 [ 3 5 6 9 7 ]
4회전 결과 [ 3 5 6 7 9 ]
버블정렬
각 단계마다 가장 큰 키 값을 갖는 레코드를 마지막에 위치
예) 초기배열 [6, 4, 9, 2, 3, 8]
1회전 결과 [ 4 6 2 3 8 9 ]
2회전 결과 [ 4 2 3 6 8 9 ]
3회전 결과 [ 2 3 4 6 8 9 ]
4회전 결과 [ 2 3 4 6 8 9 ] , * 4회전 수행 후 교체 일어나지 않으므로 정렬이 완성된 것으로 인식하여 끝난다.
삽입정렬
- 정렬 대상의 크기만큼 추가공간은 필요없다. 추가공간이 필요한 것은 2-way 합병정렬이다.
- 이미 정렬돼 있을 경우 빠르다.
예) 초기 배열 [ 7, 6, 3, 9, 4 ]
| 정렬 리스트 | 정렬되지 않은 리스트 |
|
| 초기 단계 | 7 | 6 3 9 4 |
| 1회전 결과 | 6 7 | 3 9 4 |
| 2회전 결과 | 3 6 7 | 9 4 |
| 3회전 결과 | 3 6 7 9 | 4 |
| 4회전 결과 | 3 4 6 7 9 |
퀵정렬
- 분할방식 정복법으로 동작
- 구현은 재귀함수 호출 포함
| 이진 탐색 트리 | 균형 O(logn) | 불균형 O(n) |
| AVL 트리 | O(logn) | |
| 해싱 | 완전해싱 O(1) | 충돌발생 O(n) |
트리
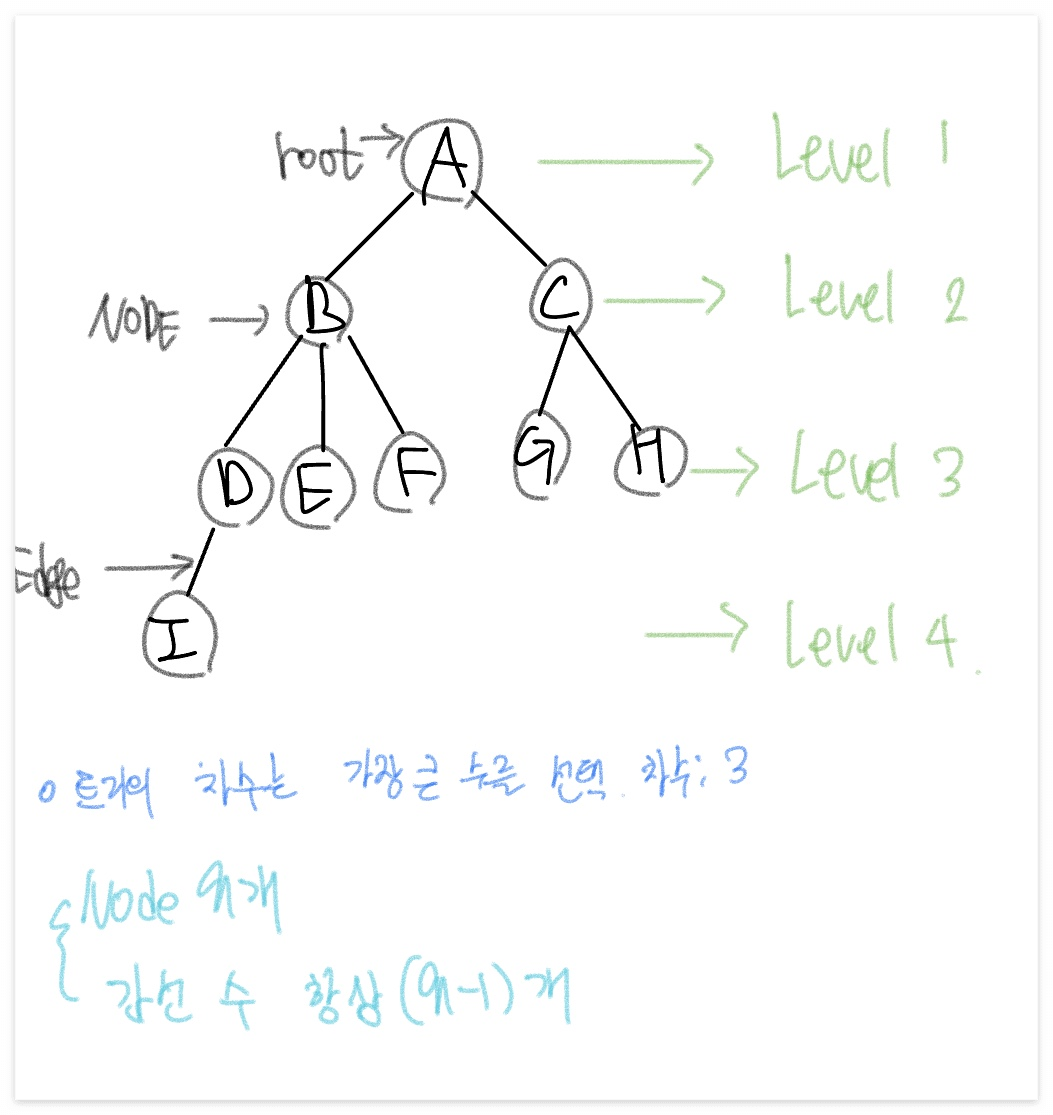
- 차수 (Degree) : 파생된 직계 노드의 수
- 높이는 0부터 시작한다. 높이 3
트리 순회
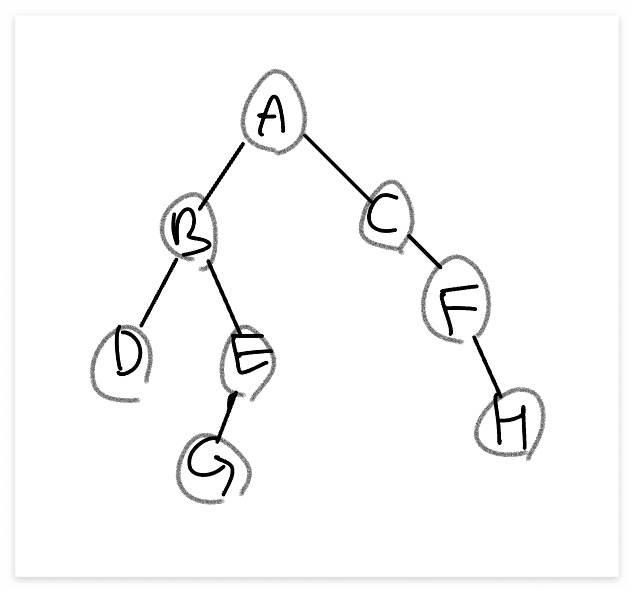
* 루트 노드의 위치를 생각하기
- 전위 순회 (Preorder traversal) / Root-Left-Right
결과: A B D E G C F H
- 중위 순회 (Inorder traversal) / Left- Root-Right
결과: D B G E A C F H
- 후위 순회 (Postorder traversal) / Left-Right- Root
결과: D G E B H F C A
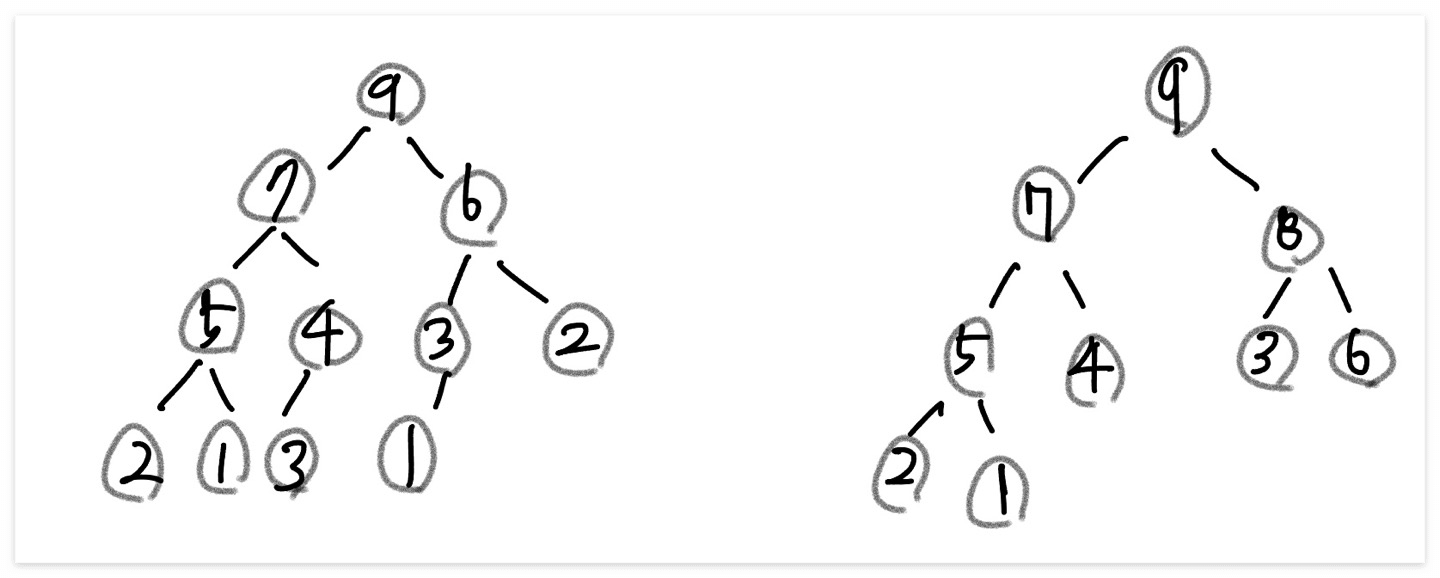
최대 힙 트리
완전이진트리 형태이면서 부노드의 값이 자노드의 값보다 작지 않아야 한다.
- 힙 삽입 삭제 모두 O(logn)
- 최소/최대값 검색 : O(1)
- heapify : O(n)
- 최대 힙 트리에서 노드를 한개 삭제하는 경우
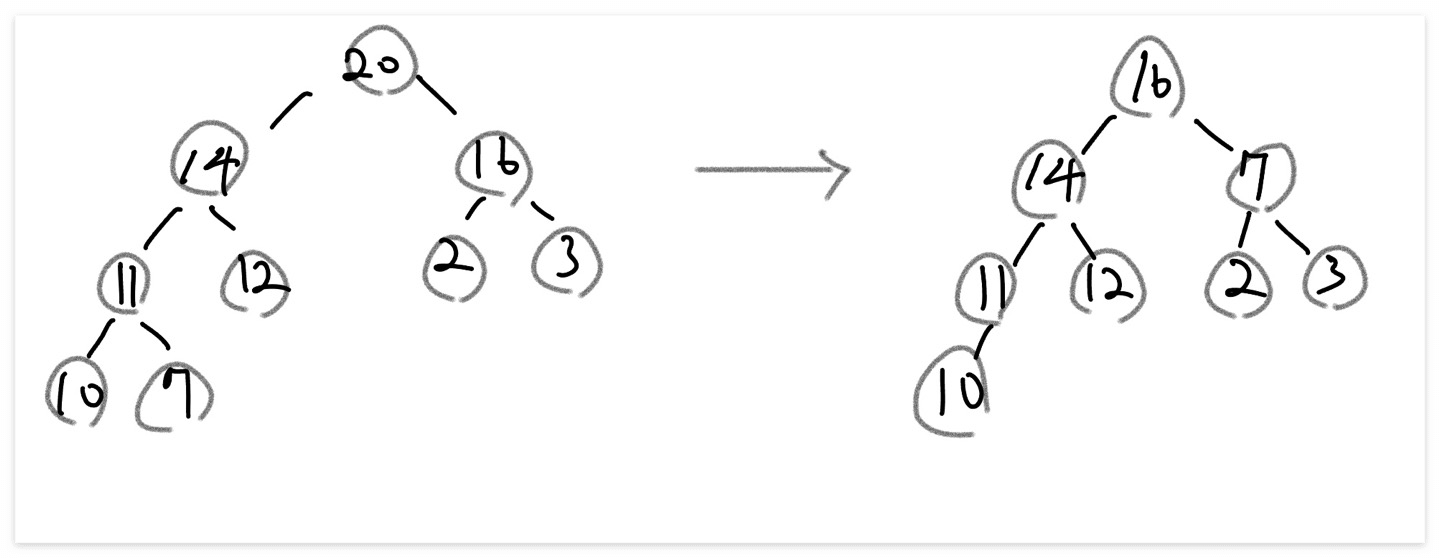
삭제 연산을 수행하기 위해 우선 루트노드인 20을 삭제한다. 일단 마지막 노드인 7이 그 자리에 위치한다.
이후 루트노드(7)과 자노드를 비교하여 큰 값이 16이 루트가 되고 7은 자노드로 이동한다.
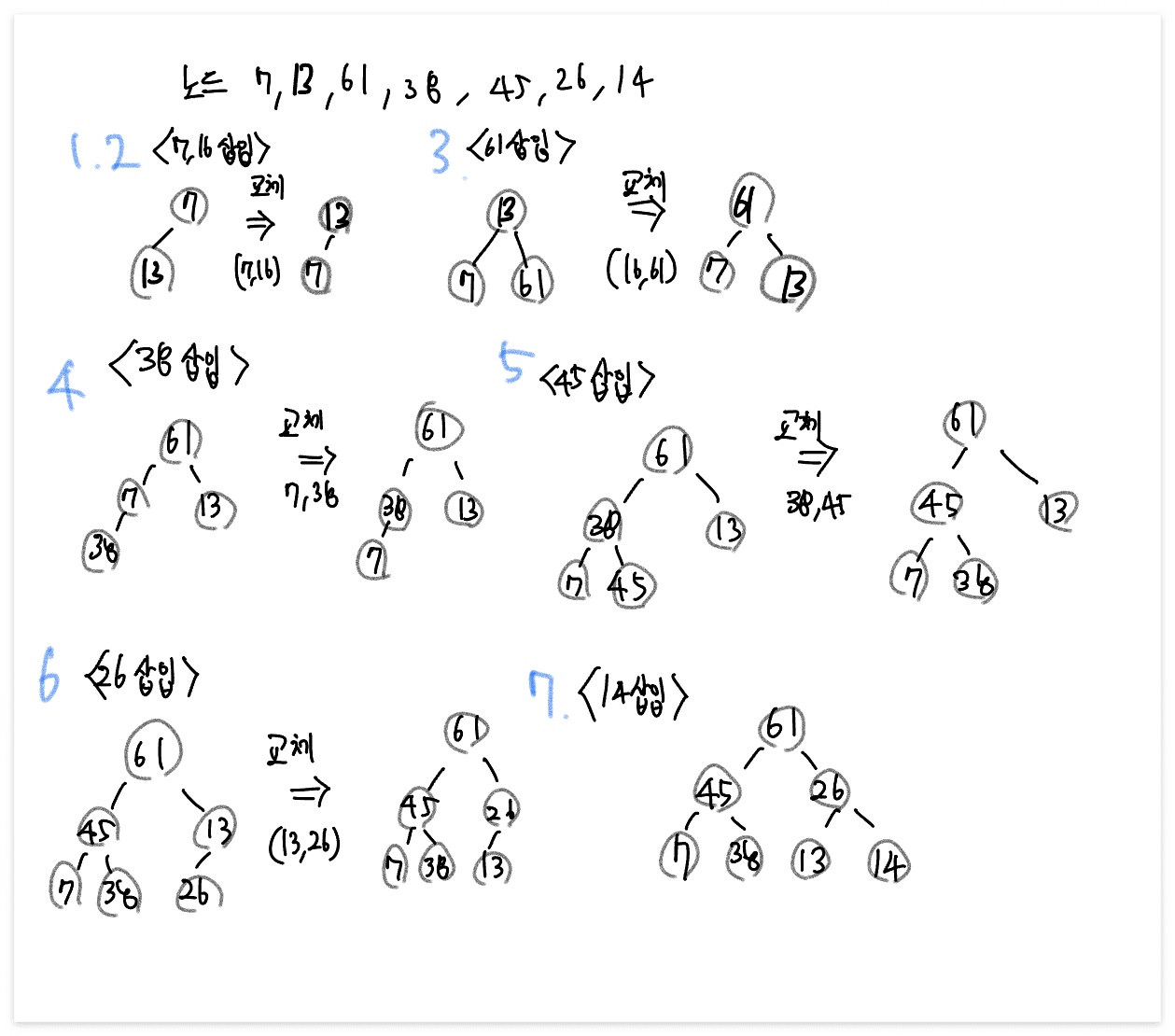
노드 7, 13, 61, 38, 45, 26, 14 를 차례대로 삽입하여 최대 힙 구현
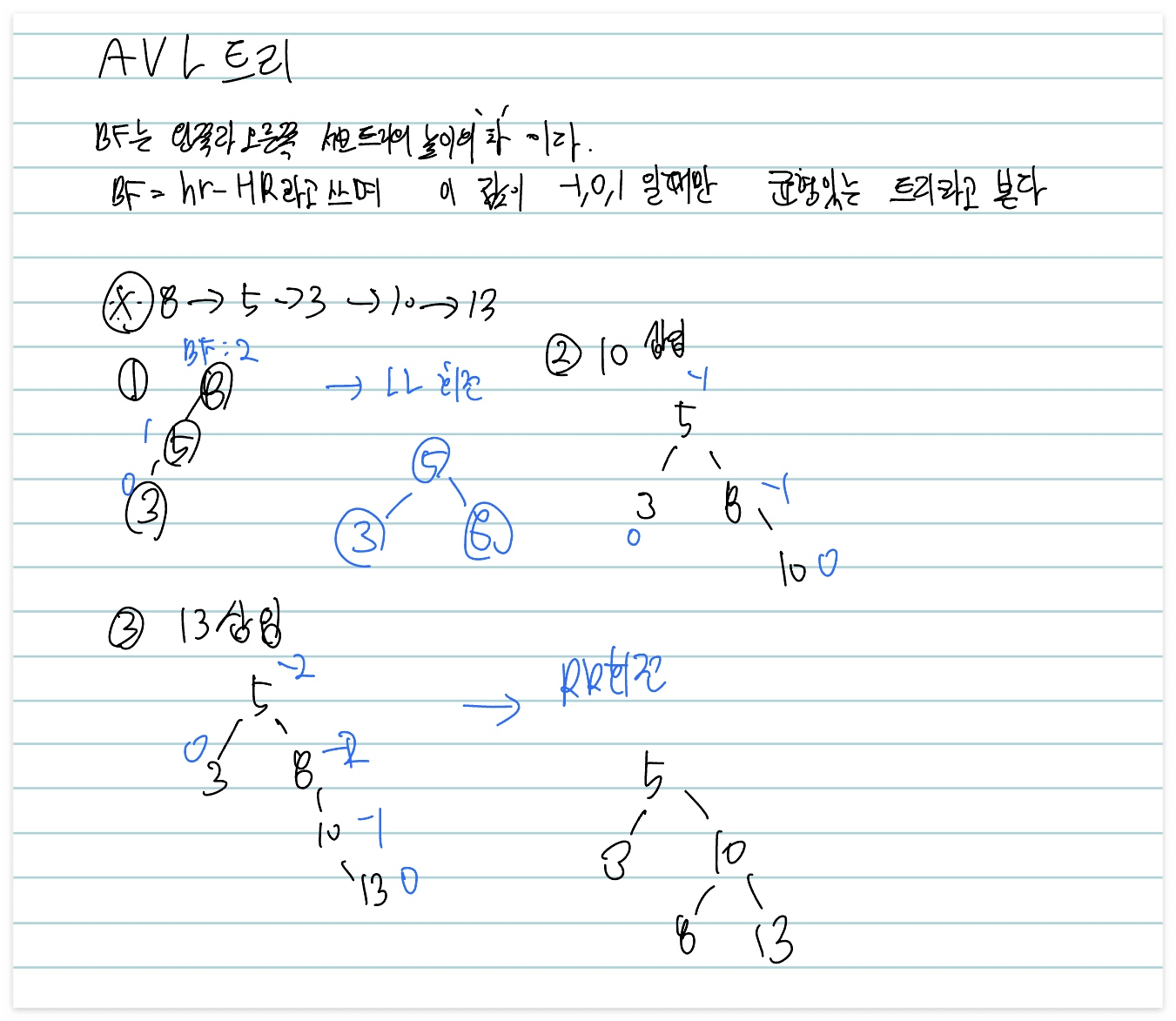
AVL 트리
해싱
키 값의 계수적인 성질을 이용하여 저장주소를 구한 후 자료를 저장하고 같은 방법으로 자료의 검색, 삽입, 삭제 등을 수행하는 방법. 삭제 삽입이 용이하고 빠름
* 해싱 기법의 용어 정리
- 버킷: 해싱함수에 의해 계산된 주소에 자료를 기억시키기 위한 기억 장소
- 슬롯: 한개의 레코드를 저장할 수 있는 공간, n개의 슬롯이 모여 하나의 버킷을 이룸
- 오버플로 : 충돌이 발생하고 해당 주소 버킷이 가득 차서 빈 슬롯이 없는 경우
* 해싱 함수의 종류
-제산법: 버킷의 수에 근접하는 수로 키 값을 나눈 나머지를 홈주소로 사용
-기수 변환법: 다른 기수 값으로 변환하여 그 값을 이용
참고
- '컴퓨터일반 기출문제집' 박미진 편저